【例题38:教材例4-31】某投资项目现金流量信息如下:NCF0=-100(万元),NCF1-10=20(万元)。根据上述资料,计算该项目的内部收益率。
| 利率 | 年金现值系数 |
| 14% | 5.2161 |
| 16% | 4.8332 |
-100+20×(P/A,IRR,10)=0
(P/A,IRR,10)=100/20=5
运用内插法
| 利率 | 年金现值系数 |
| 14% | 5.2161 |
| IRR | 5 |
| 16% | 4.8332 |

IRR=15.13%
(2)一般方法:逐次测试法
估计折现率代入净现值的计算公式,
若净现值=0,内部收益率=估计的折现率
若净现值>0, 内部收益率>估计的折现率
若净现值<0, 内部收益率<估计的折现率
若经过有限次测试,仍未求得内部收益率IRR,则可利用最为接近零的两个净现值正负临界值NPVm NPVm+1及其对应的折现率rm、rm+1四个数据,应用内插法计算近似的内部收益率。
即,如果以下关系成立:

通过上式,可解出内部收益率IRR
【例题39】接教材例4—27,某项目的所得税前净现金流量数据如下:NCF0-1为-50万元,NCF2-11为20万元。该项目的基准折现率为10%,计算该项目的内部收益率(所得税前)。
【解析】
NPV=20×(P/A,IRR,10)×(P/F,IRR,1)-50(P/F,IRR,1)-50
=0
估计折现率10%,计算净现值如下:
NPV=20×(P/A,10%,10)×(P/F,10%,1)-50(P/F,10%,1)-50
=16.2648(万元)
估计折现率12%,计算净现值如下:
NPV=20×(P/A,12%,10)×(P/F,12%,1)-50(P/F,12%,1)-50
=20×5.6502×0.8929-50×0.8929-50
=6.2562(万元)
估计折现率14%,计算净现值如下:
NPV=20×(P/A,14%,10)×(P/F,14%,1)-50(P/F,14%,1)-50
=20×5.2161×0.8772-50×0.8772-50
=-2.3487(万元)
运用内插法计算如下:
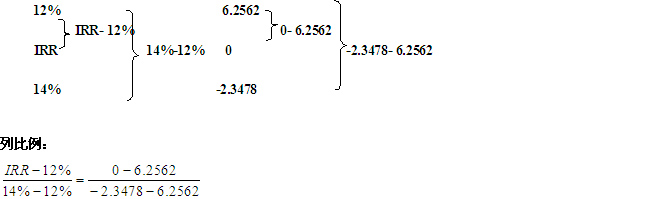
IRR=13.45%
(3)插入函数法
3、内部收益率优缺点:
优点:既可以从动态的角度直接反映投资项目的实际收益水平,又不受基准收益率高低的影响,比较客观;
缺点:计算过程复杂。
4、内部收益率评价:只有内部收益率指标大于或等于行业基准收益率或资金成本的投资项目才具有财务可行性。
总结:
动态指标之间的关系
净现值、净现值率、获利指数和内部收益率指标之间存在同方向变动关系。即:
当净现值>0时,净现值率