- 计算各方案的净现值
- 比较各方案的计算期,并确定最短的计算期
- 计算除最短计算期方案之外的其他方案的年等额回收额
- 按最短计算期将各方案的年等额回收额折算为净现值
- 比较调整后的净现值,选择调整后净现值最大的方案为最优方案
- B方案的最短项目计算期为10年,
要求:
(1)判断每个方案的财务可行性;
(2)用年等额净回收额法作出最终的投资决策(计算结果保留两位小数)。
【解答】
(1)判断方案的财务可行性
因为A方案和B方案的净现值均大于零
所以这两个方案具有财务可行性
因为C方案的净现值小于零
所以该方案不具有财务可行性
(2)比较决策
A方案的年等额净回收额=958.7/(P/A,10%,11)=147.6(万元)
B方案的年等额净回收额=920/(P/A,10%,10)=149.7(万元)
因为149.7>147.6
所以B方案优于A方案
【例题47:教材4-39】
| 1 | 2 | 3 | 4-9 | 10 | 11-14 | 15 | 净现值 | |
| A | -700 | -700 | 480 | 480 | 600 | - | - | 756.48 |
| B | -1500 | -1700 | -800 | 900 | 900 | 900 | 1400 | 795.54 |
【解析】
计算思路:
(1)计算各方案的净现值
(2)确定最小公倍数,从而确定方案重复次数
(3)计算调整后的净现值
(4)比较调整后的净现值,选择调整后净现值大的方案为最优方案
A方案的项目计算期为10年,B方案的项目计算期为15年,最小公倍数为30。
在此期间,A方案重复两次,B方案重复一次。
A方案
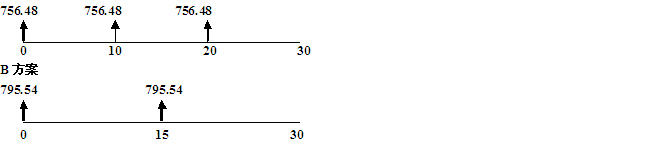
NPVa’=756.48+756.48×(P/F,12%,10)+756.48×(P/F,12%,20)=1078.47
NPVb’=795.54+795.54×(P/F,12%,15)=940.88
NPVa’> NPVb’,所以A方案优于B方案
上述题目用最短计算期法决策:
计算思路:
NPVb’=795.54×(A/P,12%,15)×(P/A,12%,10)
=718.07
NPVa’> NPVb’,所以A方案优于B方案
【例题48:06年多选】在项目计算期不同的情况下,能够应用于多个互斥投资方案比较决策的方法有()。
A.差额投资